Полигони

[kamenf]

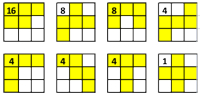
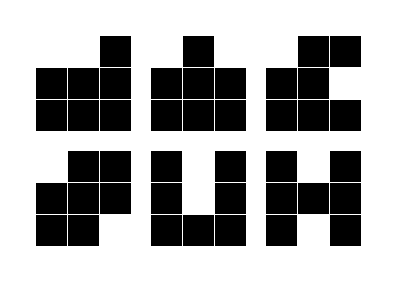Дадено е квадратно поле от 4х4 точки.

●  ●  ●  ●

●  ●  ●  ●

●  ●  ●  ●

●  ●  ●  ●

Затворен полигон в това поле е такъв, чийто страни са само хоризонтални и вертикални отсечки с краища някоя от точките от полето, без пресичания и прекъсвания на контура.

Например:

●––●––●  ●       ●––●––●  ●           
|     |          |     |   
●––●  ●––●       ●––●  ●  ●
   |     |   и      |  |
●  ●––●––●       ●––●  ●––●
                 |        | 
●  ●  ●  ●       ●––●––●––●

но не и:

●––●––●  ●         ●––●––●  ●
|     |            |     |   
●––●––●––●         ●––●––●  ●
      |  |   или      
●  ●  ●––●         ●––●––●––●
                   |        | 
●  ●  ●  ●         ●––●––●––●

Колко е броя на възможните затворени полигони (два еднакви полигона минаващи през различни точки се броят за два)? И нека не е само число, но и подплатено с някакво аналитично, логично или подобно обяснително решение.

[Bibi]

Още не знам какво ще броим, но е ясно, че от всяка точка трябва да излизат точно 0 или 2 клечки. Условието за едносвързаност трябва да се включи допълнително.
От всички забранени фигури най-особена ми се вижда тази, която прилича на 0 - голям квадрат с издупчен малък квадрат в средата.
Още: има хляб за индукция. Ако сме решили задачата за мрежа 3х3, можем да броим по колко начина можем да я издължим до 4х4.

[ql^2/8]

Според мен задачата се състои в това да преброим "тетрисчетата", които
могат да се изрежат от квадратче 3х3. Под "тетрисчета" разбирам всички
различни фигурки, съставени от 1, 2 ... до 9 квадратчета, които не се разпадат на части
и нямат вътрешни изрязани области. По ред на номерата от 1 до 9 преброих:
брой - площ:
1 х 1
1 х 2
2 х 3
4 х 4
8 х 5
8 х 6
4 х 7
2 х 8
1 х 9

или общо 31 фигурки.

[kamenf]

А как броим по колко начина се разполага всяко едно от тези 31 "тетрисчета" в квадрата? Щото търсим това, всъщност (ако ще гледаме полигоните като "тетрисчета" де).

[ql^2/8]

Не съм прочел добре условието. Сега разбирам, че трябва да се броят и
траслации, ротации и огледални изображения...

[ql^2/8]

Намерих време да преброя и положението на тетрисчетата.
Получих общо 185 варианта, ако не съм объркал нещо.
Най-много са при 6-триксчетата: 48, а по реда на номерата от 1 до 9:
9 - 12 - 22 - 28 - 45 - 48 - 12 - 8 - 1
Сега ми кажи, че има значение и началната точка на полигона и посоката на въртене...

[Bibi]

както и дали го рисуваш с лява/дясна ръка и с какъв цвят писалка
Всъщност тези, дето са с площ 4, не са ли 6 различни? В долната таблица си писал, че са 4. (две с формата на Г, две като Z, едно Т и едно каре). Освен ако смяташ огледалните образи като еднакви.
Също така аз изброих 6 или 7 (зависи от тълкуването) различни фигурки с площ 7, а при теб са само 4. И тук имам предвид без да броя симетриите. Това дава 30 (вместо 12) варианта.

[kamenf]

Сега ми кажи, че има значение и началната точка на полигона и посоката на въртене...

Завъртяни, отместени, огледални - все са различни полигони.

Всъщност тези, дето са с площ 4, не са ли 6 различни?

Ако не ги връткаме и "отгледалваме" (брех, че хубава дума ) са 4, инак зависи от възможните завъртания и "огледалвания".

[ql^2/8]

@Bibi
Тези с площ 4 наистина са 6, но две от тях са огледални и първоначално ги приех за еднакви. (после се поправих!)
Тези с площ 7 са 6 броя, но при две от тях полигонът се самопресича, остават 4.

При две от тях - ротацията дава 4 възможности, другите две, завъртени на 180 градуса съвпадат със себе си, имат само две положения.
2х4+2х2=12

[Bibi]

За случая 7:

@Камене, тази самопресича ли се по условие:

докосва се, но това дали се смята за проблем?

[kamenf]

Ами простичко казано, щом може да се изпълнят по два начина, значи не е чисто нещо и приемаме, че се пресичат. Ти го беше казала най-добре - от възел или 2, или 0 отсечки - така няма място за двоумения

[ql^2/8]

Ами да - изтървал съм тия, несиметричните.

Те добавят всяко по 8 нови полигона - с въртене и отражение.
Станаха за 7-триксчета: 28 броя.

[Bibi]

Това се нарича "едносвързано". За протоклола

За случая с площ 5, не са ли само 44?
Другите са ясни, само за 6 не съм гледала.

http://www.mathedpage.org/puzzles/polyo/

[ql^2/8]

За случая с площ 5, не са ли само 44?

Сега като ме питаш за 5, ги изкарах 49:

[kamenf]

Така, май, лека-полека ще се стигне до някаква бройка. Ама като гледам много лека-полека и някак си несигурно. А как ли ще е ако е по-голямо полето?!