Преговор на материала (носталгично)

[ql^2/8]

Като се порових из форума назад, реших да извадя отново няколко
задачи, които като че ли не са достигнали до приемливо решение.
Може пък с днешния акъл да се сетим нещо, пък и нови хора влизат...

1. Зайци и салати от моркови.
Имаме 1000 чинии със салата от моркови, две от салатите са отровни.
Отровата е достатъчно силна в произволна концентрация за хора и зайци.
Имаме 10 опитни зайчета, с които да тестваме салатите.
Времето, с което разполагаме ще ни стигне само за един опит - даваме
на зайчетата да опитат някакъв набор салати, изчакваме да подейства и
веднага след това трябва да сервираме.
Можем ли да определим 900 гарантирано безопасни салати?


* * *


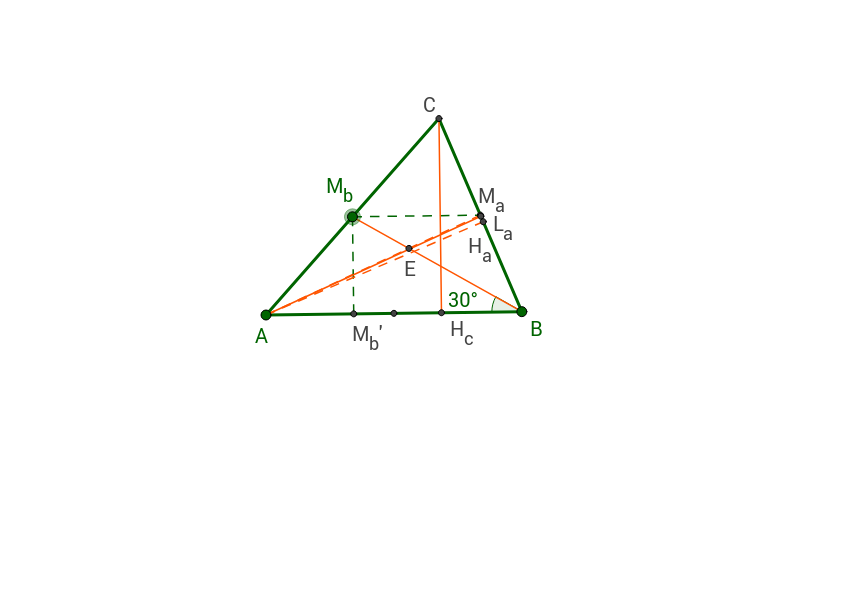
2. Задача 284 (Равностранен триъгълник)
Да се докаже, че ако в триъгълник АВС ъглополовящата при ъгъл А, медианата от
върха В и височината от върха С са равни, то триъгълникът е равностранен.
Имате право да ползвате материала, изучен до 7-ми клас!


* * *


3. Задача за теста
Тест се състои от 30 въпроса с два възможни отговора - верен и неверен.
При всеки опит ученик отговаря на всички въпроси и получава в резултат
броя на верните отговори. В началото ученикът няма никаква идея относно
верните отговори. Тестът остава един и същ. Колко е минималният
брой опити за да може гарантирано да познае всички верни отговори?

* * *


4. Задача за картината
Имаме картина с достатъчно дълга връвчица, двата края на която
са завързани отгоре за картината и 3 пирона, забити в стената. Да се
закрепи картината към стената с всичките 3 пирона така, че при
изваждането на който и да е от тях тя да падне на земята.
Триенето се пренебрегва! (оригиналната задача е за N пирона)

[ql^2/8]

Пълно мълчание в тази тема?

Жокер по задачата за картината:

Теория на връвчиците

Нека означим два пирона с А и Б




Ако означим с +А заобикаляне на връвчицата по часовата стрелка около
пирон А. С -А означаваме завъртането обратно на часовата стрелка.
Да извадим пирон, означава съответните операции да изчезнат от
поредицата.


Ясно е, че ако имаме последователни противоположни операции
те веднага се анулират - първа картинка.
+А-А = 0


Обаче, ако операциите не са последователни,
те не се съкращават: +А+Б-А не е равно на Б - втора картинка.
Ако махнем пирон Б - остава +A-A, което се разплита.
Ако махнем пирон А - остава +Б - и си виси.


Да видим как е при
+А+Б-А-Б - третата картинка.
Който и пирон да извадим - картината пада.

Виждам ли някой да опита с три пирона?

[MitkoS]

+c (+a+b-a-b) -c (+b+a-b-a)

[ql^2/8]

Ами да, с тоя жокер убих задачата...
За повече от 3 пирона ако има желаещи, могат да
съставят алгоритъм. Аз не съм програмист, а инженер,
затова ще нарисувам на MitkoS решението:

[MitkoS]

След жокера, наистина стана доста лесно ... поне що се отнася до "символното разписване и решаване".

За N пирона става по индукция

p_n - с това означавам n-тия пирон
S(n) - с това означавам поредицата с която се решава за n-пирон
S^-1(n) - с това означавам поредицата с която се решава за n-пирон, но записана в обратен ред.

При такива означения решението за пирон номер n+1 се записва така

S(n+1) = +p_n+1 S(n) -p_n+1 S^-1(n)

.... като че ли първо трябва да се докаже пак по индукция, че ако S(n) е решение за n на брой пирони, то S^-1(n) също е решение.
И след това е очевидно, че S(n+1) е решение така както е записано по-горе.

ПП.
Аватара ми е поизрязан кадър от филма "13-тия етаж"

ПП.
За момент се изкуших да напиша, че S^-1(n) е все едно стената е прозрачна и сме застанали от другата страна, така че S^-1(n) е очевидно решение и не е нужно да се доказва, че е такова.
Но всъщност, в общия случай не е вярно, че е S^-1(n) е равносилно на обратната страна на прозрачна стена. И затова го изтрих.

[kamenf]

Дадено:
- триъгълник ABC.
- CH_c - височина
- AL_a - ъглополовяща на ∠A
- BM_b - медиана на AC
- CH_c = AL_a = BM_b

Нека M_bM_b' е перпендикулярна на AB, тогава тя е и 1/2 от CH_c (M_b е среда на AC). Триъгтлника BM_bM_b' е правоъгълен с катет M_bM_b' = 1/2 BM_b => ъгъл ABM_b = 30°

Да разгледаме трапеца ABM_aM_b (M_a среда на BC).

1. Нека ∠A > ∠B. Тогава AM_a < BM_b, но тъй като медианата на тръигиник е по-голяма или равна на ъглополовящата при същия ъгъл, следва, че в този случай и AL_a < BM_b, което противоречи на условието.

2. Нека ∠A = ∠B. Тогава ∠A = ∠B = 60° (∠AEM_b = 60°, от отношенията в равнобефрен трапец AE/EM_b = AB/M_aM_b = 1/2 => ΔAEM_b е правоъгълен => ∠EAM_b = 30°) => AL_a съвпада с AM_a.

3. Нека ∠A < ∠B. Тогава в ΔABC BC<AB (∠B>60°, ако L_b е пресечната на ъглополовящата на ∠B с AC, то CL_b < CM_b и следователно от отношението на страните към частите на отсечките от ъглополовящата BC<AB). Тогава от лице на триъгилник CH_c*AB = AH_a*BC и предишното следва, че CH_c < AH_a, но височината тябва да е по-малка или равна на ъглополовяшата, т.е. AH_a <= AL_a откъдето CH_c < AL_a което противоречи на условието.

Следователно единствената възможност е 2. и триъгълник на който два ъгъла са 60° е равностранен.

ПП: Поправена правописна грешка с именуване на правилия ъгъл B в т.3

[ql^2/8]

3. Нека ∠A < ∠B. Тогава в ΔABC BC<AB (∠A>60°, ако L_b е пресечната на ъглополовящата на ∠B с AC, то CL_b < CM_b ...

Ето тук не ми е ясно:
1. Защо ∠A>60° ?
2. Защо CL_b < CM_b ? - според мен е обратното, L_b е между M_b и А, защото AB е най-малката страна.

Изобщо при дадения триъгълник и твоите разсъждения е ясно, че най-малката страна е срещу височината,
следващата срещу ъглополовящата и най-голямата срещу медианата, като разбира се, равенствата също са вариант.

[kamenf]

Ето тук не ми е ясно:
1. Защо ∠A>60° ?
2. Защо CL_b < CM_b ? - според мен е обратното, L_b е между M_b и А, защото AB е най-малката страна.

Изобщо при дадения триъгълник и твоите разсъждения е ясно, че най-малката страна е срещу височината,
следващата срещу ъглополовящата и най-голямата срещу медианата, като разбира се, равенствата също са вариант.

1. Правописна грешка - ∠B>60°. Не забравяме, че все още разглеждаме трапеца. В т.2 ∠A=∠B=60°. Естествено, че при същите основи, и диагонал, който сключва 30° с тях, когато ∠A<∠B, ∠B>60°. За по-подробно могат да се разгледат два трапеца с обща основа, другите основи - равни и наполовина на долната и диагонал сключващ 30° с основите - единият - равнобедрен, а другият - с различни ъгли, по-специално ∠A<∠B:

2. Мисля, че сега е ясно, че CL_b < CM_b.

- - - - - - - - - -

...защото AB е най-малката страна.

Това изобщо не виждам откъде следва, а и не мисля, че е толкова очевидно да се докаже дори за случая когато е.

Изобщо при дадения триъгълник и твоите разсъждения е ясно, че най-малката страна е срещу височината,
следващата срещу ъглополовящата и най-голямата срещу медианата, като разбира се, равенствата също са вариант.

Това също не мисля, че може да се каже толкова лесно. Поне аз не се сешам за някаква теорема учена до седми клас от която да следва нещо такова. Или ако има някоя за отношение на височините към основите, най-малкото не можем да кажем двете неизвестни височини как се отнасят една към друга просто знаейки какви са отношенията между ъглополовящата при едната и медианата при другата.

[ql^2/8]

Това че AB е най-малката страна е очевидно:
Тъй като височината е най-късата отсечка между върха и срещуположната страна,
то височините от ъглите A и B са по-къси от съответните медиана и ъглополовяща,
които пък са равни на височината от ъгъл C. Излиза, че височината от ъгъл С е най-голямата
от всички височини. От формулата за лице по страна и височина, следва срещу най-голямата
височина да стои най-късата страна.

- - - - - - - - - -

1. Нека ∠A > ∠B. Тогава AM_a < BM_b

Ако това твърдение е вярно (лесно се доказва), то срещу по-голямата страна,
(тази, срещу по-големия ъгъл A) има по-малка медиана. (1)

...тъй като медианата на триъгълик е по-голяма или равна на ъглополовящата при същия ъгъл...

(и това лесно се доказва) (2)

Ще рече, че при два върха с равни ъглополовяща и медиана, този с
ъглополовящата има по-голяма или равна медиана от другия (според 2),
и съответно по-малка срещуположна страна (според 1).

[ql^2/8]

Малко теория на тестовете:


Нека броят на отговорите "да" в група "X" означаваме с "x".
Ще наричаме "x" тегло на "Х".
"Претегляне" на една група въпроси ще наречем пускането на
теста с "да" за тези въпроси, а останалите с "не".


Ако претеглим цялата група N ще получим общото тегло n.
След това претегляйки какъвто и да е набор А от k въпроси,
получаваме отговор R, чрез който можем да изчислим теглото на "A"
R = N - n + a - (k - a)
2a = R + n - N + k


Жокер:
Ако за с 2 опита решаваме тест с 2 въпроса,
с 4 опита решаваме тест с 5 въпроса,
колко голям тест ще решим с 8 опита?