Квадратчета в квадрата

[ql^2/8]

Задача:
Имаме бял квадрат разграфен на 5х5 малки квадратчета.
Трябва да оцветим минимален брой малки квадратчета
така, че във всеки квадрат 3х3, част от големия
да има точно 4 оцветени.

[XIIID]

която е да е шарка от 4, повтаряща се през всеки 3 квадратчета по хоризонтала и вертикала. Кога са най-малко... не ми се мисли сега.

- - - - - - - - - -

... освен да ги натъпча някак в ъгъла на десена ли...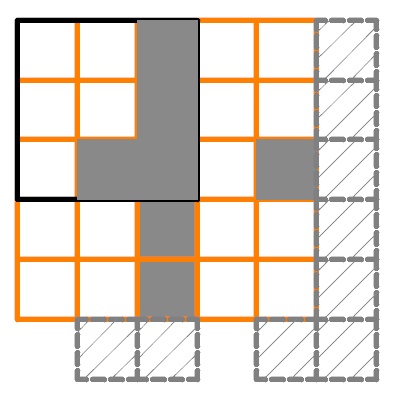

[MitkoS]

9 на брой

[XIIID]

моите са 7

[spiritch]

И аз стигнах до 7

[ql^2/8]

Някой ще предложи ли 6? Или ще докаже, че по-малко от 7 не може.

[XIIID]

Някой ще предложи ли 6?

Аз няма

От повтаряемостта на клетките при копиране през 3 в двете посоки се вижда, че минимумът е 2+2+2+1.

Сега, ако някой има нерви да предложи комбинации извън предложената от мен схема на редуване, да заповяда. На 45 съм, пипето ми деградира прогресивно вече 20-та година...

[Bibi]

Няма решение с по-малко от 7.
По условие в горния ляв 3х3 квадрат има 4 оцветени. В долния десен - също, но те имат само едно общо блокче, значи поне 3 са нови.

[ql^2/8]

Bibi даде оригиналното доказателство за минималност.
XIIID даде схемата (втората) със 7 квадратчета, която доказва
че е възможно.
Браво и на двамата!