Подгряващи задачи

[ql^2/8]

Понеже в другата тема има оглушително мълчание, тук ще пусна две
подгряващи задачки с доста по-малка трудност:

1. Задача за 4 заека
Имаме 4 заека и 64 салати, от които 1 отровена.
Един опит се състои в това:
Даваме на зайците да опитат някакъв набор салати, изчакваме един час
и в резултат зайците, които са опитали отровената салата умират.
Тогава планираме следващия опит.

Какъв е минималният брой опити, с които можем с точност
да установим отровената салата?
Какъв максимален брой салати можем да тестваме с този брой опити?

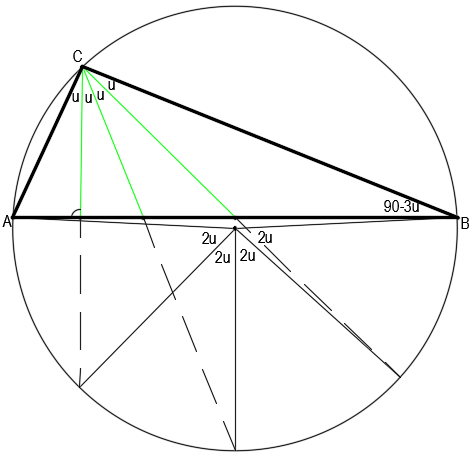
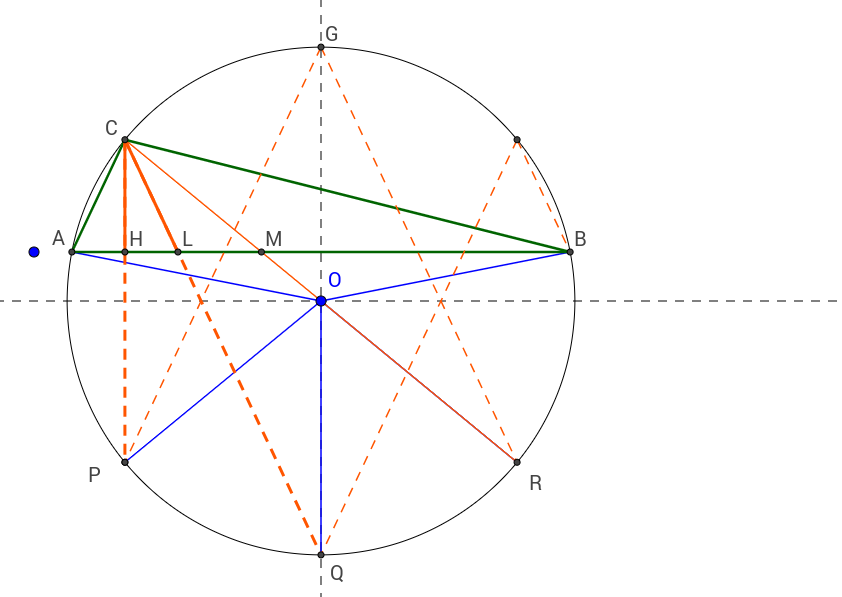
2. Специален триъгълник:
В триъгълник височината, ъглополовящата и медианата
при един и същи връх разделят ъгъла на 4 равни части.
Да се намерят ъглите в триъгълника.
(По възможност без тригонометрия!)

[Kx]

При късмет може да определим само с 1 един опит.
Ако искаме винаги да можем да определим ни трябват 4 опита,( докато измрат зайците)
Максималния брой салати е 120 за тези 4 зайци (опита)

[XIIID]

[ql^2/8]

Да кажем, че има опити за отговори, но няма решения.

[XIIID]

Да кажем, че има опити за отговори, но няма решения.

?!

Sent from my Amazon Kindle Fire using Tapatalk

[ql^2/8]

Решение е нещо такова:
Продължих трите "ъгло-на-4-делящи" до пресичане с описаната окръжност и свързах точките с центъра и.
Знам, че централните ъгли са два пъти по-големи от вътрешните...
И после?

[MitkoS]

Според мен, примера с правоъгълен триъгълник с остър ъгъл 22,5 градуса е достатъчно ясно решение. ... даже не е нужно да описваме подсказваща окръжност около него.
Елементарно се вижда (според мен), че ако вземем такъв триъгълник и "нарежем" правия ъгъл на четири еднакви части от 22,5 градуса, то новополучените отсечки са медиана, ъглополовяща и височина в основния триъгълник.
И останалата неизвестна част от задачата е (пак според мен), дали този правоъгълен триъгълник е единственото решение.

[ql^2/8]

Да, даденият чертеж илюстрира отговор на задачата.
Очевидно този отговор удовлетворява условието.
Но не и достигането до него.
* * *
На другата задача имаме отговор 4 опита. Пак без решение.
Засега никой не оспорва...

[kamenf]

Нека имаме произволна окръжност с център O в която построяваме 4 еднакви съседни централни ъгъла (започвайки от произволна точка A от окръжността) ∠AOP, ∠POQ, ∠QOS и ∠SOB. Построяваме перпендикуляр през т. P към отсечката AB който се пресича с нея в т. H и с окръжността в т. C. Така получената CH се явява височина в триъгълника ΔABC. CL (получена от CQ) се явява ъглополовяща на ъгъл ∠C в ΔABC, М е пресечната точка на CR с AB, а ъглите ∠ACH, ∠HCL, ∠LCM и ∠MCB са равни (по построение от еднаквите им съответни централни ъгли).


Ще докажем, че CR минава през точка O.


QO е перпендикулярна на AB (ъглополовяща в равнобедрения триъгилник ΔAOB) и следователно успоредна на PC. От тук следва, че ъгъл ∠PCQ = ∠CQG. ∠CQG = ∠QGR (∠PCQ и ∠QGR имат еднакви централни ъгли). Следователно CQ е успоредна на GR , откъдето следва, че четириъгълника CQRG на който две от страните са успоредни, а единият диагонал QG минава през центъра на описаната около него окръжност се явява правоъгълник и следователно CR (другият му диагонал) минава през т. O. С това доказахме, че CM минава през т. O и единствената възможност триъгълник в който М да е среда на AB e тя да съвпада с O или с други думи основата му AB да е диаметър. Такъв триъгълник е правоъгълен и от тук следва, че 1/4 от правия му ъгъл ∠C e 22.5 градуса, ъгъл А е 90-22.5=67.5, а ъгъл B = 22.5.

[Kx]

Ето описани на опитите
1 опит , салатите се разделят на 5 (4x 13 салати е една с 12) В най- лошия случай умира заек от една ял от 13 салати ( остават 3 заека)
2 опит делим 13те салати на 4 ( 3х3 и една 4) . Всеки заек яде от 3те салати, в най-лошия случай умира заек и имаме 3 салати (2 остават 2 заека)
3.1 ако са останили 2 заека/3салати . даваме им по една салата и една остава
3.2 ако са останали 3 заека / 4 салати даваме на всеки заек по салата и остава една
==> 3 опита са достатъчни.

[sclera_bg]

Решението на дъщеря ми за означенията по-горе (все пак има малко геометрия)

Нека AH = x , и LM = y . Тогава HL = x , а MB = 2x+y.

Прилагаме свойството на ъглополoвящата както следва:
За ∆ ACB: AC/CB = 2*x/(2*x+2*y) [1].

За ∆ LCB: CL/CB = y/(2*x+y) [2].

От [1] и [2] следва съотношението AC/CB * CB/CL = 2*x*(2*x+y)/(2*x+2*y)*y [3] .

Съкращаваме CB в лявата част на [3] и получаваме
AC/CL = 4*x^2+2*x*y/2*x*y+2y^2 [4].

Но AC=CL, и тогава [4] може да бъде опростено до
4*x^2 = 2*y^2 или √2x = y [5].

За ∆ HCM: CH/CM = x/y = 1/√2 [6].

Aко означим CH с h от [6] следва че CM = √2*h. За същия триъгълник прилагаме Питагоровата теорема : 2*h^2 = h^2 + HM^2 или HM = h = CH, тоест триъгълника HCM е равнобедрен правоъгълен триъгълник и ∠HCM = 45° и оттам следва всичко останало.

[zxc0]

По първата задача с 3 опита стигнах до 113 салати. Дано не съм сбъркал. Разписването утре, че от телефона ще е мъка.

[ql^2/8]

Доказателствата по задачата с триъгълника се приемат!
* * *
За задачата със зайците дотук имаме доказателство за 3 опита от Kx.
Някой ще предложи ли по-малко?

[Kx]

Като се замисля мога да постигна отговора на първата задача с 2 опита, ако мога да номерирам зайците и салатите

С 3 заека мога да определя дали 1 от 8 салати е отровна по следния начин. на всеки заек давам по една салата , на заек 1 и 2 давам салата 4, на 1и3 -->5 . 2 и 3-->6. на 3те--> 7 и салата 8 остава . ако никой не умре салата 8 е отровна. ако умрат всички салата 7 е отровна. Съответно ако умрат 1,2 --> салата 4 отровна, 1,3 --> салата 5 е отровна , 2,3 --> 6 е отровна. Ако умра само някой от 1 до 3 то съответната салата е отровна.

Аналогично с 2 заека може да определим 1 от 4 салати, С 1 заек- 2 салати

При 64 салати може да ги разделим
на 4 по 8 салати + 6 по 4 салати + 4х 2салати
като на заек 1 до 4 дадем по едно от групите по 8 салати
на двойките зайци(1,2)(1,3) .... (3,4) дадем от групите по 4 салати
на тройките зайци(1,2,3), (1,2,4) ( 1,3,4) (2,3,4) дадем от групите по 2 салати
В зависимост коя група заек/зайци умре ще знаем коя е групата с отровна салата. И ще имаме достатъчно зайци за да установим от втори опит коя е отровната салата.
Както се вижда може да имаме още 16 салати които да установим с един опит с 4 заека, коя е отровна.==> 80 салати с 4 заека и 2 опита,

[zxc0]

Ееейй, пак ме изпревари и аз го измислих с 2 опита до 81 салати.

Първи опит : Даваме този набор от салати на съответният заек по реда.




Вариантите са 5 :
1. Никой заек не умира(Отровната салата е в останалите 16 салати ) - 16 салати 4 заека остават.
2. Само един заек умира (Отровната салата е съответно в жълтата клетка на умрелият заек) - 8 салати 3 заека остават.
3. Два заека умират (Отровната салата е съответно в зелените клетки на двата умрели заека) - 4 салати 2 заека остават.
4. Три заека умират (Отровната салата е съответно в сините клетки на трите умрели заека) - 2 салати 1 заека остават.
5. Всички зайци умират (Отровната салата е 65)


Втори опит:
Вариант 1.


Вариантите са същите :
1. Никой заек не умира - Отровната салата е 81.
2. Само един заек умира (Отровната салата е съответно в жълтата клетка на умрелият заек).
3. Два заека умират (Отровната салата е съответно в зелените клетки на двата умрели заека).
4. Три заека умират (Отровната салата е съответно в сините клетки на трите умрели заека).
5. Всички зайци умират - Отровната салата е 80.

Втори опит:

Вариант 2. Само един заек умира - 8 салати 3 заека остават.




1. Никой заек не умира - Отровната салата е 8.
2. Само един заек умира (Отровната салата е съответно в жълтата клетка на умрелият заек).
3. Два заека умират (Отровната салата е съответно в зелените клетки на двата умрели заека).
4. Всички зайци умират - Отровната салата е 7.

За другите 2 варианта мисля че е ясно вече:
3. Два заека умират (Отровната салата е съответно в зелените клетки на двата умрели заека) - 4 салати 2 заека остават.
4. Три заека умират (Отровната салата е съответно в сините клетки на трите умрели заека) - 2 салати 1 заека остават.