Съжалявам, допуснал съм техническа грешка, но мисля, че метода ми е правилен.
След като открих грешката, получавам 209 навивки с обща дължина 631.14м.
Нямам време да рисувам картинки, но ще кажа с няколко думи. Смятам дължините на 209 окръжности , първата с радиус 100см. Стъпката на намаляване на радиуса на по-горната окръжност получих от триъгълниците и ъгъла - 0.5 см. (Закръглявах)
Накрая ги сумирам и получавам 631.14 м.





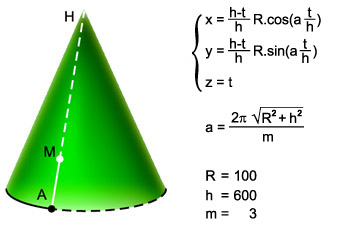 Разложих движението на две:
Разложих движението на две:


