Моето беше само идея. Щом мислите, че има хляб в нея, ще я опиша по-подробно:
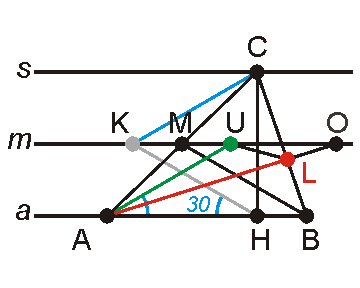
Първо чертаем три равноотдалечени успоредни прави a, m, s на разтояние h/2 една от друга.
Избираме произволна точка B от правата a.
Прекарваме през B права, сключваща с правата a ъгъл 30о и бележим точката на пресичането й с правата m с буква М. Точките B и M вече са напълно "заковани" в смисъл, че без ограничения можем да считаме, че всеки триъгълник, отговарящ на условието, че медиана и височина в него са равни, ще минава задължително през тях.
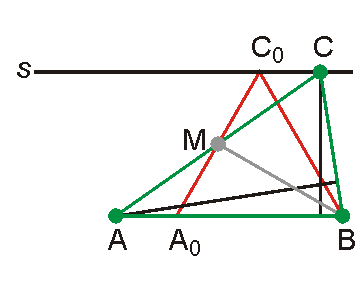
Съществува единствен такъв равностранен триъгълник, който построяваме, катопрекараме през B права, сключваща с правата a ъгъл 60о и бележим точката на пресичането й с правата s с буква Co, а след това през Co чертаем права, сключваща с правата s ъгъл 60о и бележим точката на пресичането й с правата а с буква Аo.
Значи целта ми е да докажа, че ако и ъглополовящата е равна на онези двете, тогава т. А (връх на произволен триъгълник, удовлетворяващ условията на задачата) съвпада с т. Ао.
(заради ограничението в дължината на изказванията ще продължа в следващ пост)





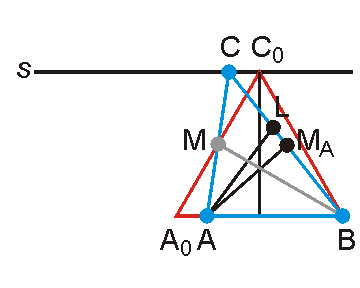
 . Разбира се ако искате да намерите друг начин (друго решение)- споделете го! Въпреки това обявявам @Bibi за победител.
. Разбира се ако искате да намерите друг начин (друго решение)- споделете го! Въпреки това обявявам @Bibi за победител.