Задача 284 (Равностранен триъгълник)

[Anubis Black]

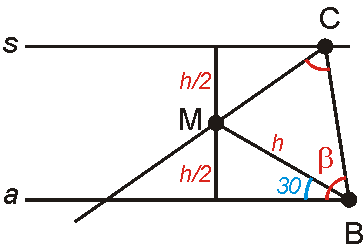
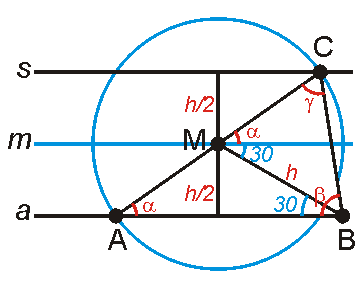
Тази задача ми я даде г-н Величков от НПМГ в 7- ми клас и каза, че ще даде 50лв. на този, който я реши. Може да ви се стори лесна, но ето и уловката- имате право да ползвате материала, изучен до 7- ми клас. Сега се поразрових и намерих едно решение, което ми го изпрати един професор по математика от Америка. Писмото му започва така: "..., задачата е много силна. Мисля, че и преди съм я засичал, но чак сега я реших...", след което следват леми и някакви други глупости, които не разбирам и разбира се г-на не ми прие решението и останах на сухо . Няколко години се опитвах да я реша, но безуспешно. Използвах какво ли не- дори имах чертеж, на който знаех всички ъгли! Вие сте последната ми надежда (Obi- Wan Kenobi, you're my only hope!)! А ето я и задачата:
Да се докаже, че ако в триъгълник АВС la= mb= hc, то триъгълникът е равностранен.

[MitkoS]

Може ли малко пояснения за тия дето не разбираме чак толкова тези науки.
la - какво е ?
mb - какво е ?
hc - какво е ?
Също така да предполагаме ли, че върховете на триъгълника са АВС, а страните съответно a, b, и c ?

[Edin_Lud]

la е ъглополовящата при ъгъл А, която пресича страната а
mb е медианата към страна b, която започва от ъгъл В
hc е височината към страна с, която започва от ъгъл С

Т.е. имаме триъгълник АВС със страни а (с/у ъгъл А), b (с/у ъгъл В) и с (с/у ъгъл С)

Задачата е много интересна, особено с ограничението за знания от 7ми клас. За съжаление знам как се решава - срещал съм я преди години, когато още се занимавах активно с математика.

[Gadget]

Изпревариха ме.

[MitkoS]

Благодаря, сега като го виждам написано, се сещам, че означенията са ми познати.

[MentOS]

Ееее , не , няма такава задача !!!!!!

Или аз съм тъп или наистина е лоша задачката !

[Bibi]

Означавам края на ъглополовящата с L, на медианата - M, на височината - H.
lA = AL, mB = BM, hC = CH.
Това само за да се разбираме, че не ми се чертае в момента.

Спускаме перпендикуляр от М към АВ, бележа петата му с P.
MP е средна отсечка в AHC, значи е 1/2 CH = 1/2 BM (по условие).
Тогава BMP е правоъгълен триъгълник с хипотенуза два пъти по-голяма от катета.
Така получаваме, че <ABM = 30о.
(to be continued...)

[Yasen6275]

значи е 1/2 CH = 1/2 BM (по условие).
Тогава BMP е правоъгълен триъгълник с хипотенуза два пъти по-голяма от катета.
Така получаваме, че <ABM = 30о.
(to be continued...)

Ей тези моменти ми се губи защо са така. Пояснения?

[Sugar4o]

Ей тези моменти ми се губи защо са така. Пояснения?

защото MP e успоредна на CH и* защото AM и MC са равни по условие и оттам* MP/CH=AM/AC* и тн! браво на Bibi*
оттам задачата се свежда до това дали трябва да се докаже, че медианите се пресичат в точка разделяща ги на 2:1 Ако това може да се ползва като теорема решението е готово

[Yasen6275]

В условито е дадена само една медиана. По лесно е да докажеш че всяка от трите отсечки е медиана, ъглополовяща и височина.

[Wise]

И изобщо не е толкова лесно да докажеш каквото и да е
С аналитична геометрия или вектори вероятно е лесно, но нека някой (задаващия - примерно) да каже какво е позволено.
Аз не помня подобни триъгълници в кой клас съм учил. Тригонометрия може сега в 3 клас да се учи. Та малко прецизност
няма да е излишна. Edin_Lud може да подскаже малко с какви средства разполагаме. Чичко Питагор роден ли е вече? Тригонометрията работи ли или е табу? Това на @Bibi със средна отсечка признава ли се? И ъгъл 30 градуса значи ли нещо?

А иначе условието е готино :Super:

[Bibi]

Да забравим за момент за ъглополовящата. Забелязвам, че ъгъл "бета" еднозначно определя мястото на точката C и следователно чрез него би трябвало да може да се сметне онова ъгълче "гама" горе, което съм отбелязала с червена дъга. То зависи единствено от "бета".
Но за сега нещо не мога да видя на колко е равно, а ако успеем, това ще ни даде връзка между големините на "алфа" и "бета", която ни е нужна. ("алфа" е ъгълът при А)

Питагор може, средни отсечки също, но без тригонометрия!
Ако го направиш с тригонометрия обаче, пак ще е полезно, защото нея после ще я "преведем" на езика на училищния материал...

[MitkoS]

Така като го е нарисувала Биби, една окръжност около M, с радиус AC/2 и една отсечка през М успоредна на AB (която май е и ъглополовяща на BMC), могат да се окажат доста полезни. Проблема ми е, че по никакъв начин не мога да се сетя как да използвам ъглополовящата при BАC.
// А относно оня ъгъл от 30 градуса.
Май и обратното е вярно: Ако ъгъла е 30 градуса, то височината и медианата са с равни дължини. Така че, нещо трябва да я правим ъглополовящата през BAC

[Bibi]

[Anubis Black]

Веднага мога да ви кажа какво НЕ може да се ползва от това, което сте изброили: Питагор (учи се в 9 клас); подобни триъгълници (също в 9кл.); тригонометрия (нямам идея какво представлява, но не ми звучи като нещо, което скоро ще уча ). Май дотук само средната отсечка е позволена. Аз съм свеждал задачата до доказване на един ъгъл, но това е било невъзможно. Ще се консултирам с @Bibi и тя (ако не е проблем) ще покаже няколко варианта, които съм разработил (както и варианта на една съученичка, на която дадох задачата).